Research
My research bridges AI, machine learning and high-performance scientific computing, with a focus on interpretable AI and transformative healthcare applications.
AI for Science
I’m applying state-of-the-art transformers and GPT-style models to accelerate antibody engineering, predicting mutations that boost binding affinity and streamlining the design of next-generation therapeutics. Some related work includes:
- ProtLib-Designer package : Ligthweight library for antibody design
- ProteinTuneRL : RL framework for protein design
- Science '25: Preemptive optimization of antibody escape variants
- Nature '24: Restoring antibody function with machine learning
Schematic overview of the ProtLib‑Designer pipeline for antibody library design. (From the ProtLib‑Designer paper)
I develop end-to-end ML pipelines that turn standard clinical data into actionable insights. For example, using only 12-lead ECGs, I trained deep neural networks on a dataset of 16,000+ simulated hearts to reconstruct high-resolution electroanatomical maps—potentially enabling non-invasive patient stratification previously only possible via invasive procedures. Some related work includes:
- CINC ’22: ECG to Electroanatomical Map
- 16k+ Cardiac Simulation Dataset
- US Patent on a AI-driven Electroscope
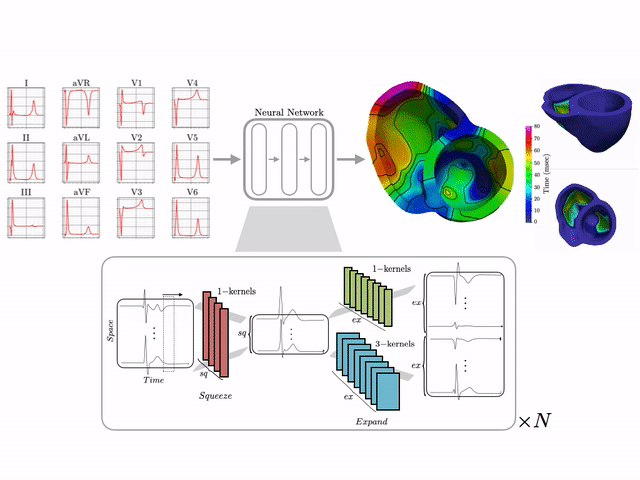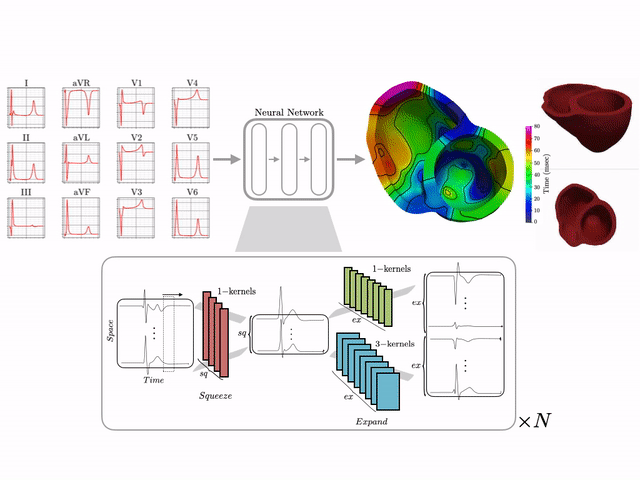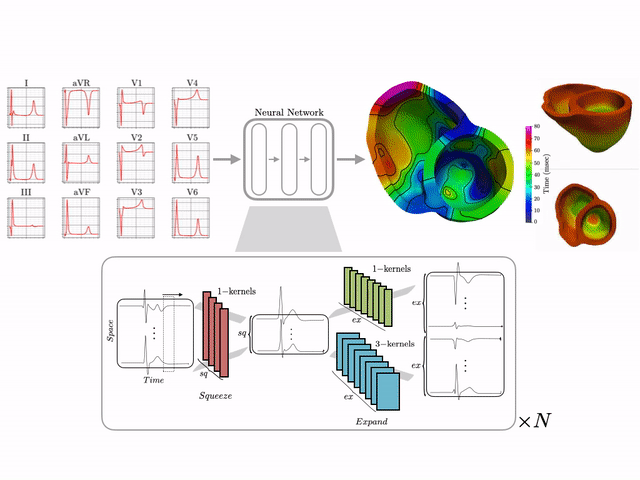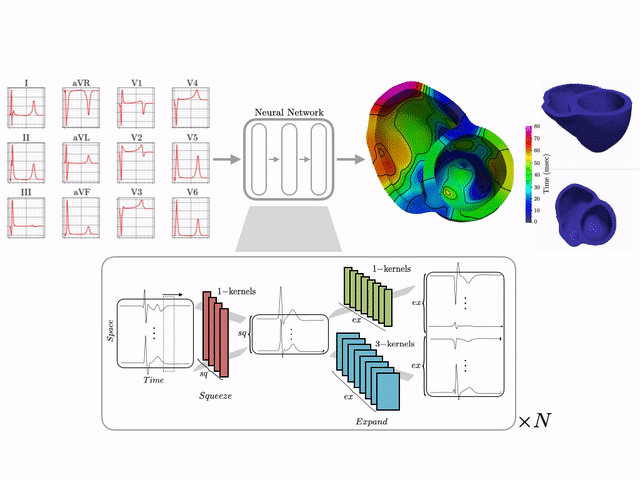
Machine learning–driven electroanatomical mapping from 12-lead ECGs. Trained on 16,000+ simulated hearts to reconstruct high-resolution cardiac structure non-invasively. (IEEE 2023 study)
Interpretability in AI
I build transparent AI models that deliver clear, auditable decisions—crucial for healthcare, finance, and regulatory environments.
I work with physicists, engineers, and biologists to extract simple, interpretable models from complex data, enabling scientific discovery and deeper understanding of underlying phenomena. Some of my work includes:
- NeurIPS ’22: Deep Symbolic Regression + Evolutionary Search
- ICLR '21: Symbolic Regression with Reinforcement Learning
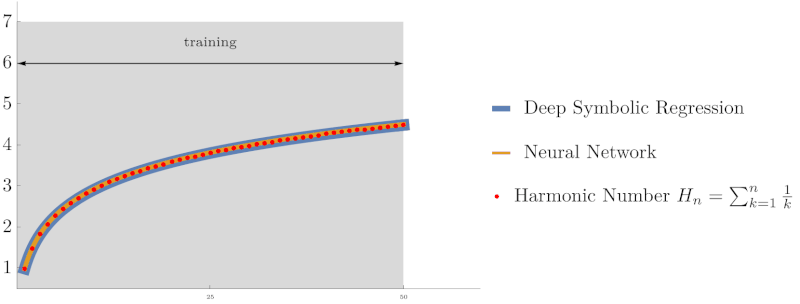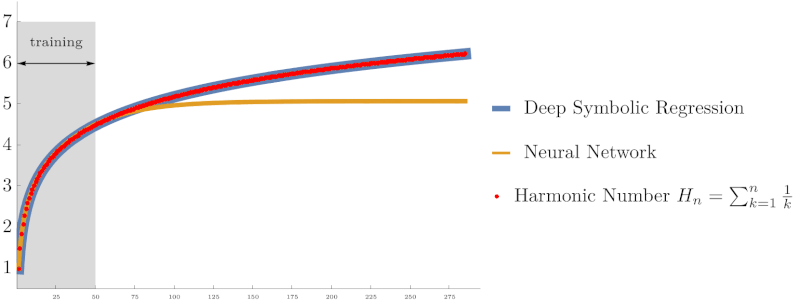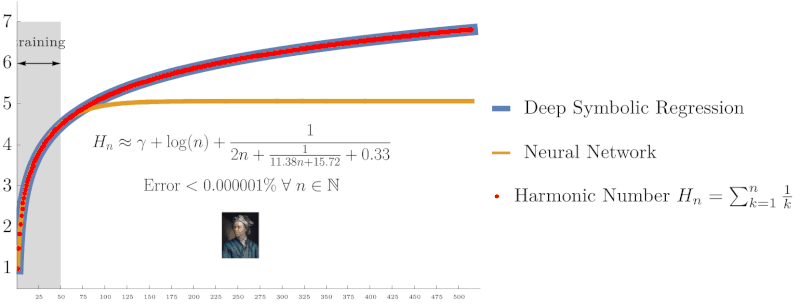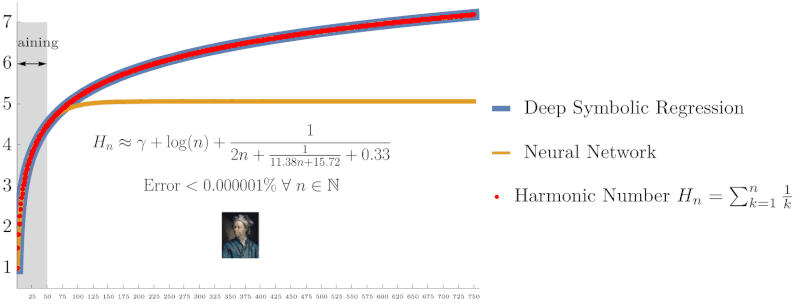
Symbolic regression using Deep Symbolic Optimization (DSO) accurately rediscovers the harmonic series identity $H_n = \sum_{k=1}^n \frac{1}{k}$ and Euler’s constant $\gamma$, outperforming neural networks in extrapolation accuracy. (From NeurIPS ’22 work on interpretable AI)
I build interpretable models that govern decision-making in complex systems, ensuring transparency and accountability. In particular, I develop decision-tree policies for reinforcement learning tasks that rival neural nets in performance while being fully transparent. Some of my work includes:
- AAAI ’25: Decision Trees for RL (with RLVR)
- GECCO ’22: 1st Place in Interpretable Symbolic Regression Competition
- ICML ’21: Interpretable Controllers for RL
Symbolic equations and decision-tree policies governing diverse reinforcement learning environments—offering transparent, high-performing alternatives to neural policies. (From AAAI ’25, ICML ’21, and GECCO ’22 work on interpretable RL)
Scientific Computing
I conduct fist-principle simulations of complex multiphysics systems, using continuum mechanics, numerical methods, and high-performance computing. I focus on optimizing both accuracy and throughput on modern HPC platforms. Some of my work includes:
- NMBI '18: Efficient Solvers for Cardiac Electrophysiology
- NMBI '16: Explicit Coupling Schemes for Fluid-Structure Interaction
- CMAME ’16: Nitsche’s Method with Cut Elements
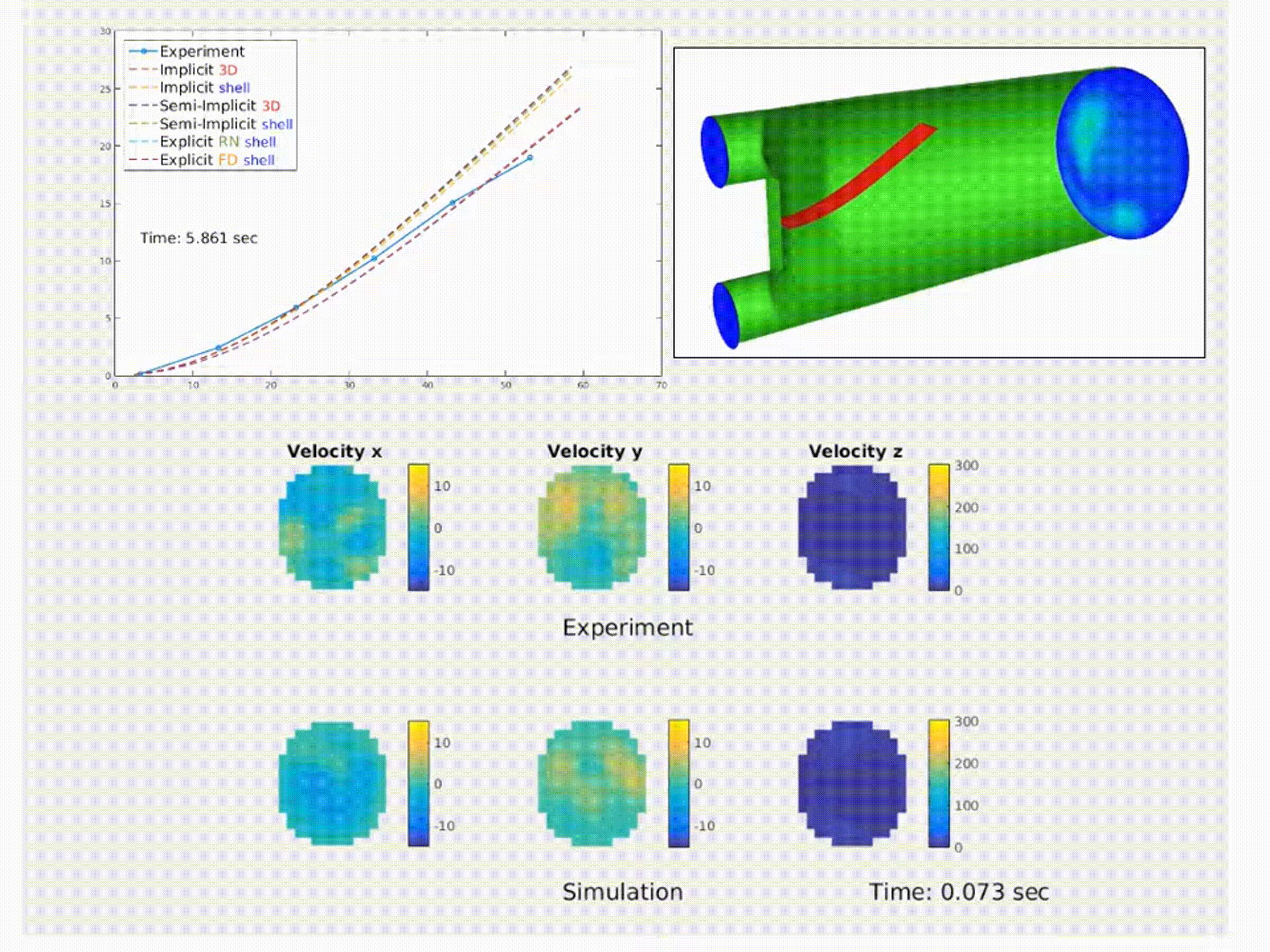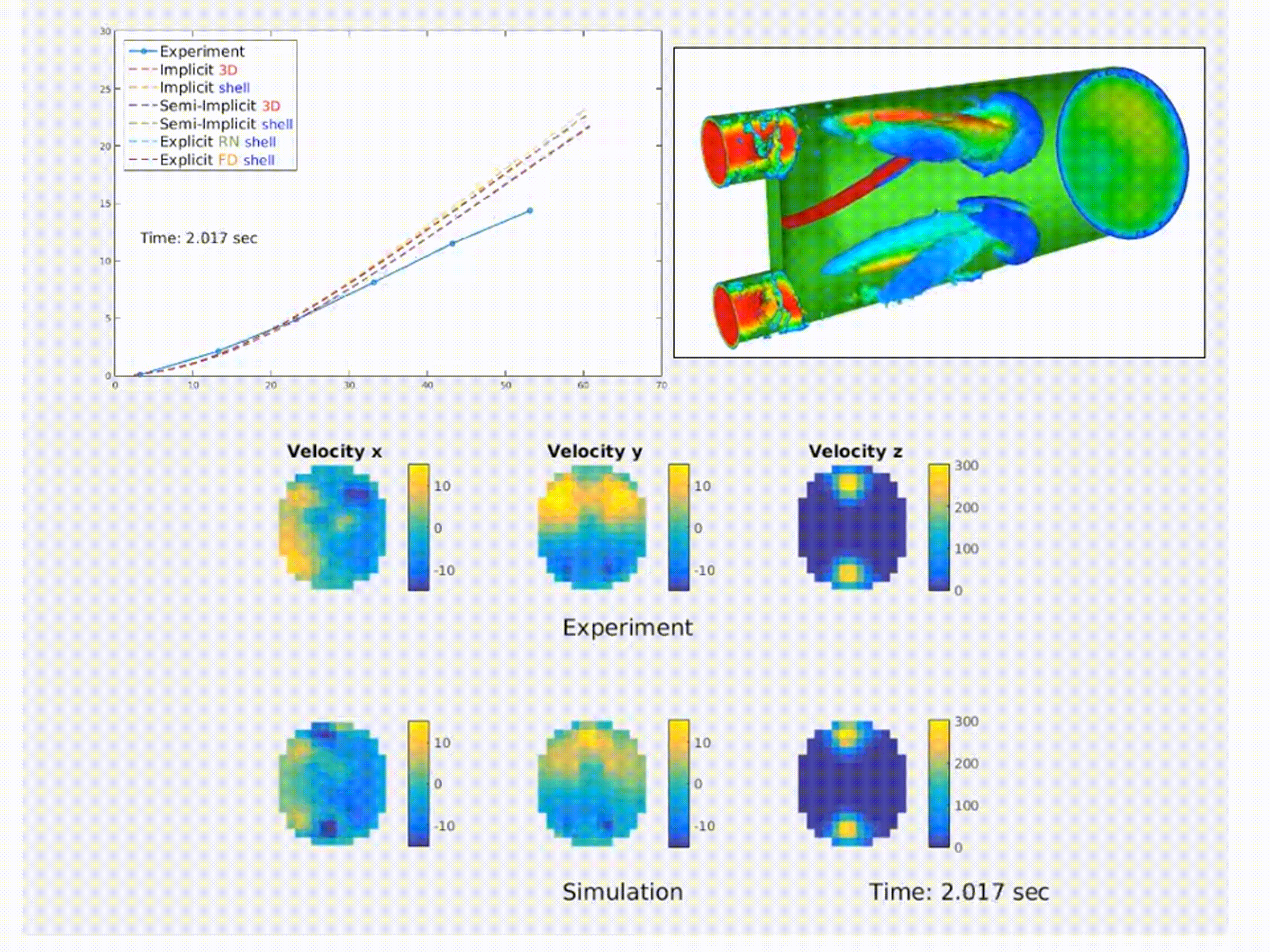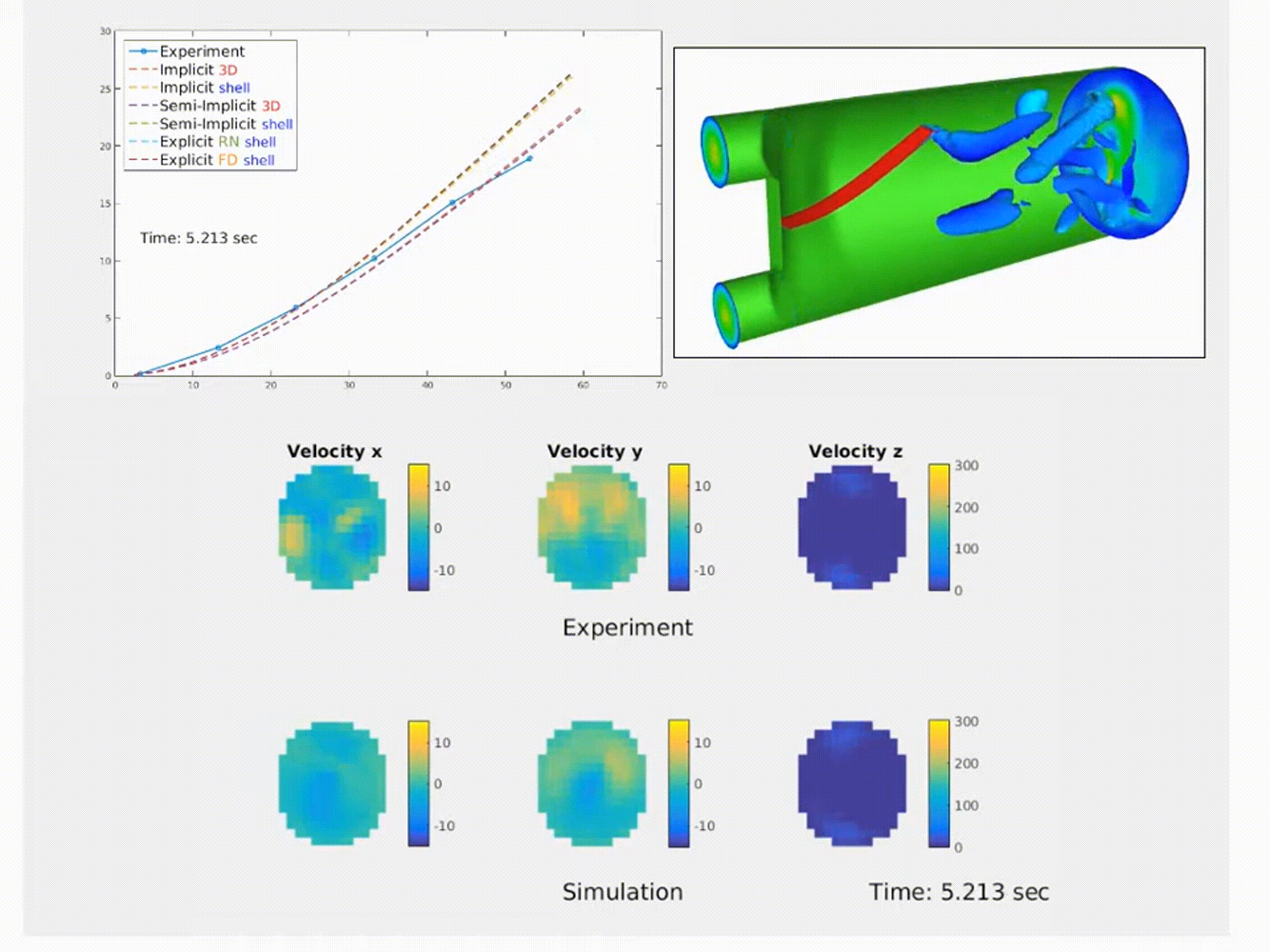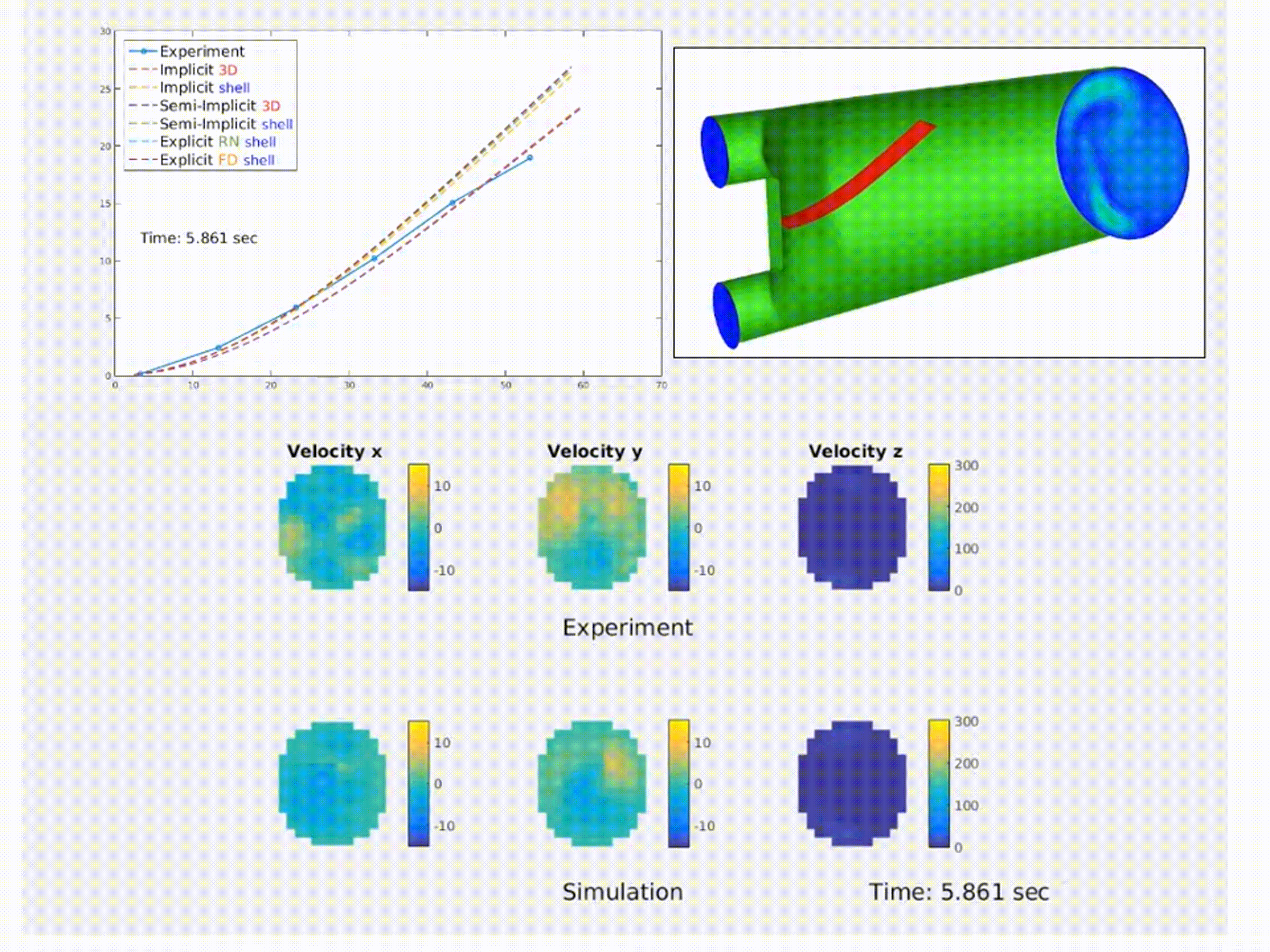
Simulation of a fluid–structure interaction (FSI) benchmark. The multiphysics model accurately reproduces experimental system dynamics using high-performance finite element solvers. (From NMBI ’18 and CMAME ’16 work on continuum mechanics and FSI)
By integrating these solvers into ML workflows, I aim to power digital twins for personalized medicine, predictive maintenance in robotics, and beyond—delivering end-to-end solutions that marry physical fidelity with data-driven speed.
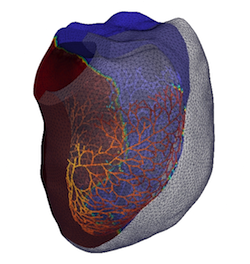
Digital twin of the human heart: high-fidelity simulation used to predict disease onset and guide personalized treatment strategies. (Part of ongoing work integrating physics-based solvers with ML pipelines)