DisCo-DSO: Joint Optimization in Hybrid Discrete-Continuous Spaces
Published:
In this blog post, we introduce DisCo-DSO (Discrete-Continuous Deep Symbolic Optimization), a novel approach for joint optimization in hybrid discrete-continuous spaces. DisCo-DSO leverages autoregressive models and deep reinforcement learning to optimize discrete tokens and continuous parameters simultaneously. This unified approach leads to more efficient optimization, robustness to non-differentiable objectives, and superior performance in tasks like decision tree learning and symbolic regression. Let’s dive into the key innovations, applications, and results of DisCo-DSO.
Optimization in hybrid discrete-continuous spaces is a fundamental challenge in AI, with applications in decision tree learning, symbolic regression, and interpretable AI. These problems often involve:
- Discrete tokens (e.g., symbolic structures or decision points).
- Continuous parameters (e.g., thresholds or constant values).
Traditional methods optimize these components separately, leading to inefficiencies and suboptimal solutions. DisCo-DSO (Discrete-Continuous Deep Symbolic Optimization), our novel approach, addresses this by jointly optimizing discrete and continuous variables.
By leveraging autoregressive models and deep reinforcement learning (RL), DisCo-DSO learns the joint distribution of these hybrid spaces. This unified approach results in fewer function evaluations, robustness to non-differentiable objectives, and superior performance.
Here’s a preview of the method in action:

DisCo-DSO generates hybrid discrete-continuous solutions in an autoregressive manner. The autoregressive modle (AR) is extended with a discrete head and a continuous head, enabling joint generation. In this example, the model generates a decision tree, where discrete tokens represent decision nodes and continuous parameters represent thresholds.
Key Innovations
DisCo-DSO builds upon the principles of deep learning and reinforcement learning, introducing two critical extensions:
- Extension of Autoregressive Models
- DisCo-DSO employs autoregressive models to generate hybrid discrete-continuous solutions by extending the model’s head to predict discrete tokens and continuous parameters conditionally. This enables the joint optimization of discrete and continuous components.
- Extension of the Risk-Seeking Policy Gradient
- DisCo-DSO introduces a risk-seeking policy gradient to handle high-variance, black-box reward functions in hybrid spaces. This extension ensures robust optimization in challenging environments with non-differentiable objectives.
- Sequential Optimization for Decision Trees
- DisCo-DSO formulates decision tree policy search in control tasks as sequential discrete-continuous optimization. It proposes a method for sequentially finding bounds for parameter ranges in decision nodes, enhancing the interpretability and efficiency of the learned policies.
Applications
DisCo-DSO is a versatile framework that can be applied to a wide range of tasks requiring optimization in hybrid discrete-continuous spaces. Hybrid optimization is common in AI for Mathematics, for example, in decision tree learning for control tasks and equation discovery for scientific applications.
Decision Tree Learning for Control
In interpretable control tasks, decision trees must optimize discrete structural decisions (e.g., splitting rules) alongside continuous parameters (e.g., thresholds).
DisCo-DSO formulates this as a sequential optimization problem, generating compact, interpretable policies. The animation below shows a decision tree applied in a control task, demonstrating the backpropagation of gradients through discrete and continuous components:
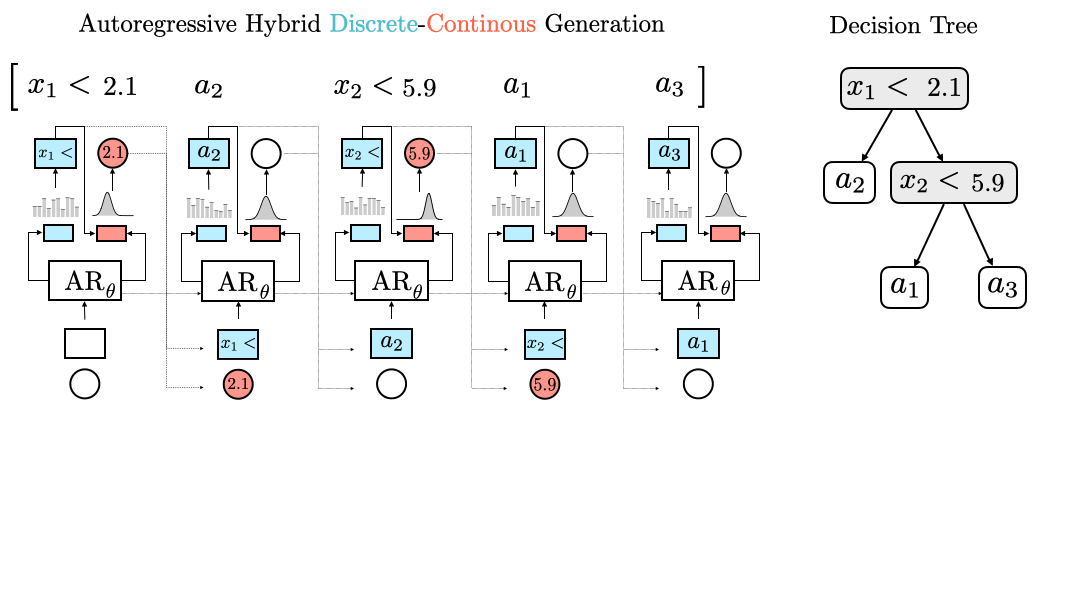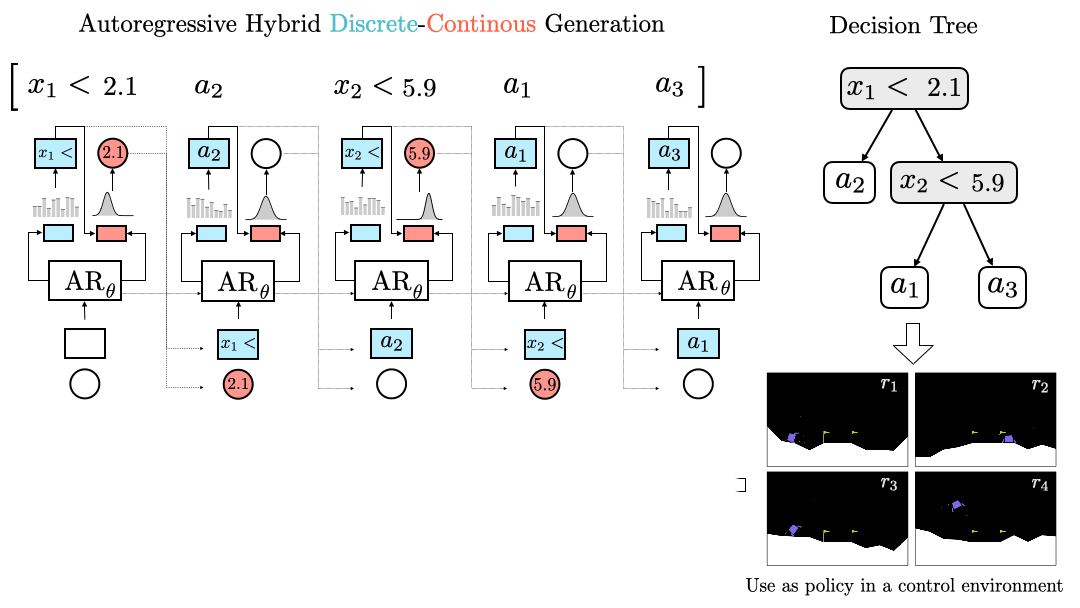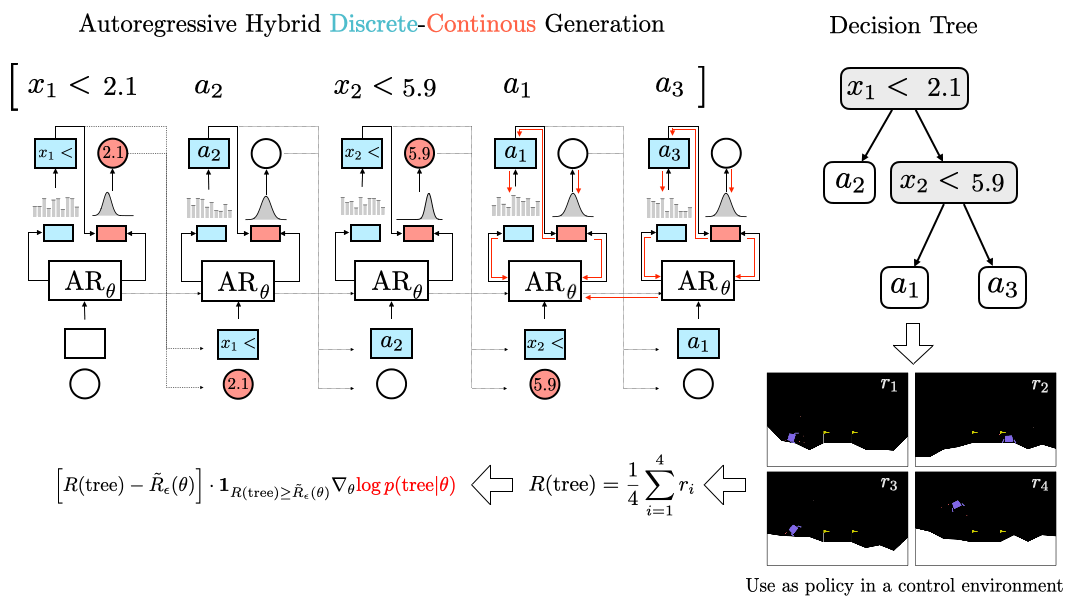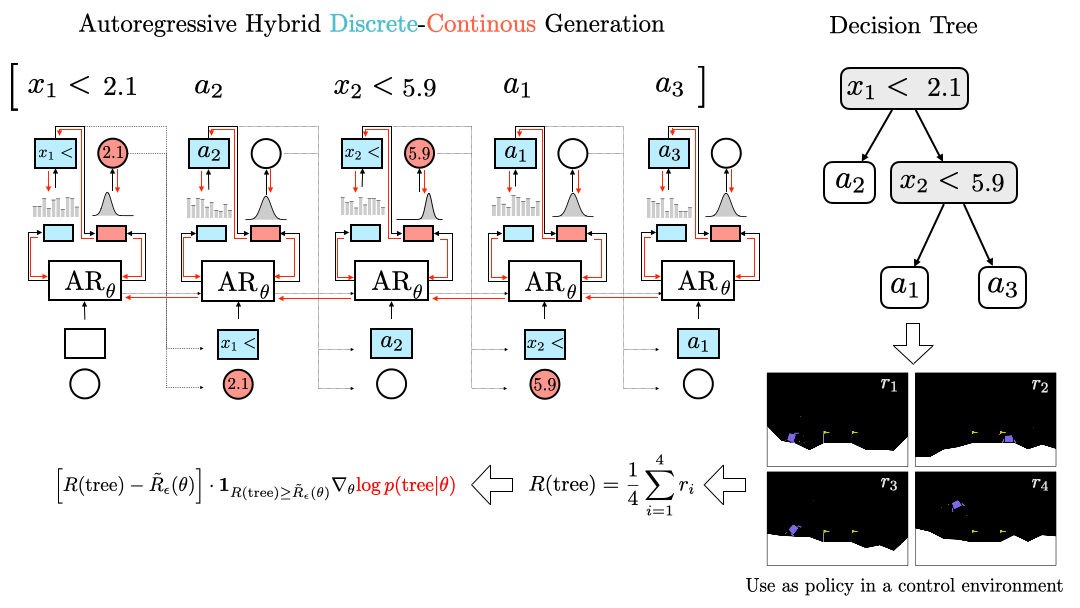
DisCo-DSO is used to optimize decision trees for control tasks. The policy represented by the decision tree is played in the environment and rewards are collected. The average reward is used to compute a top-quantile policy gradient, which is backpropagated through the model to update the parameters.
Equation Discovery for Scientific Applications
In symbolic regression, the goal is to discover mathematical equations from data. DisCo-DSO’s joint modeling approach ensures the generation of precise symbolic expressions with optimized constants, significantly improving accuracy.
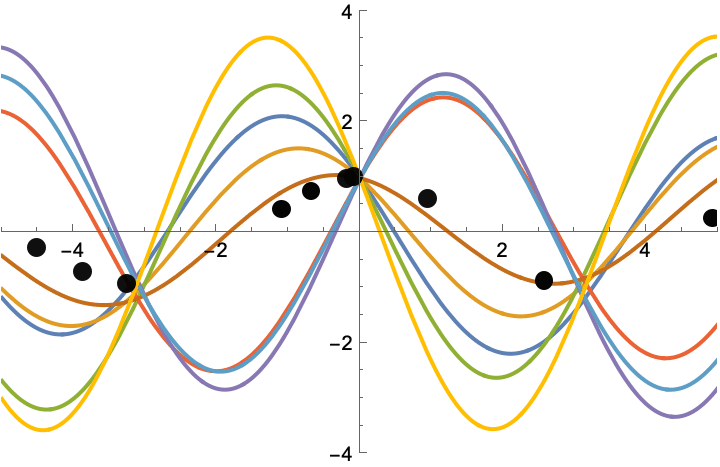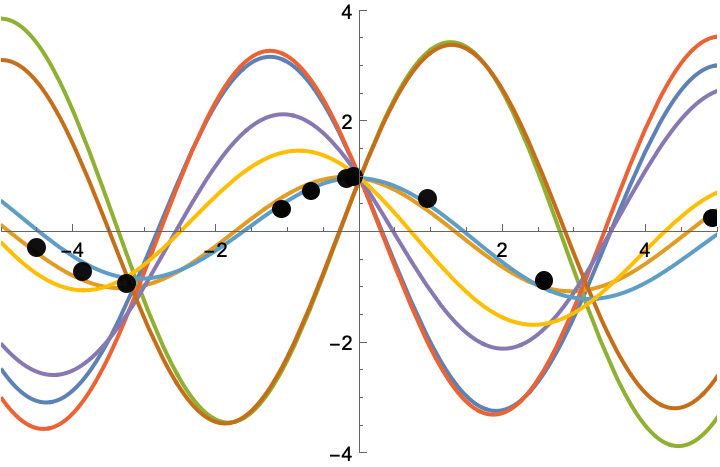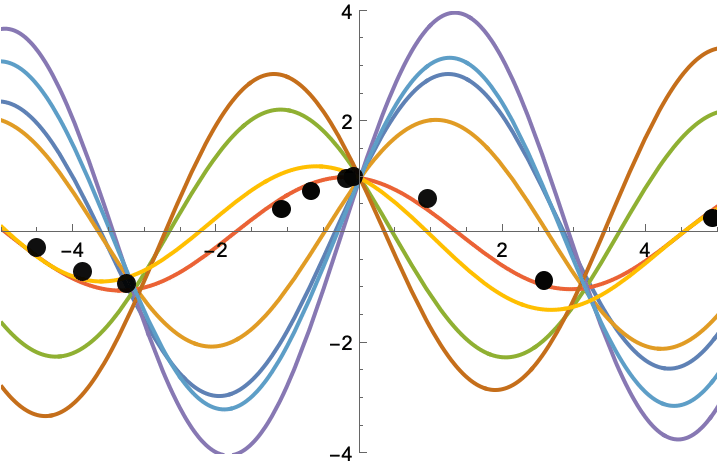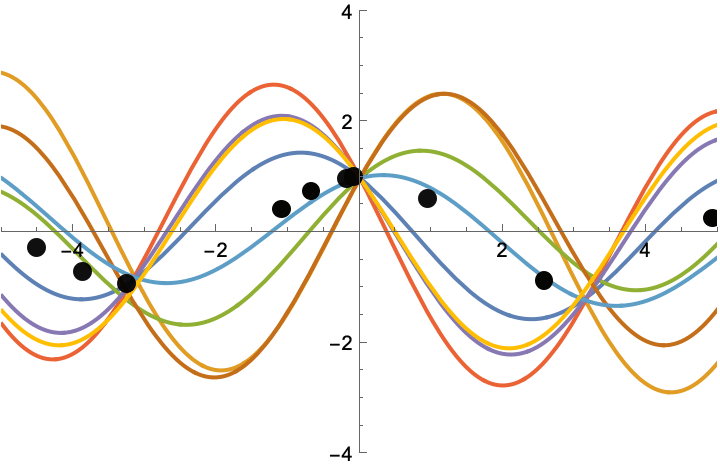
DisCo-DSO discovers symbolic equations with optimized constants to fit the data. In equation discovery tasks, a dataset of points is provided, and the model generates symbolic expressions that best approximate the data. The constants in the equations are optimized using DisCo-DSO.
Results
We evaluated DisCo-DSO on diverse tasks, demonstrating its superior performance:
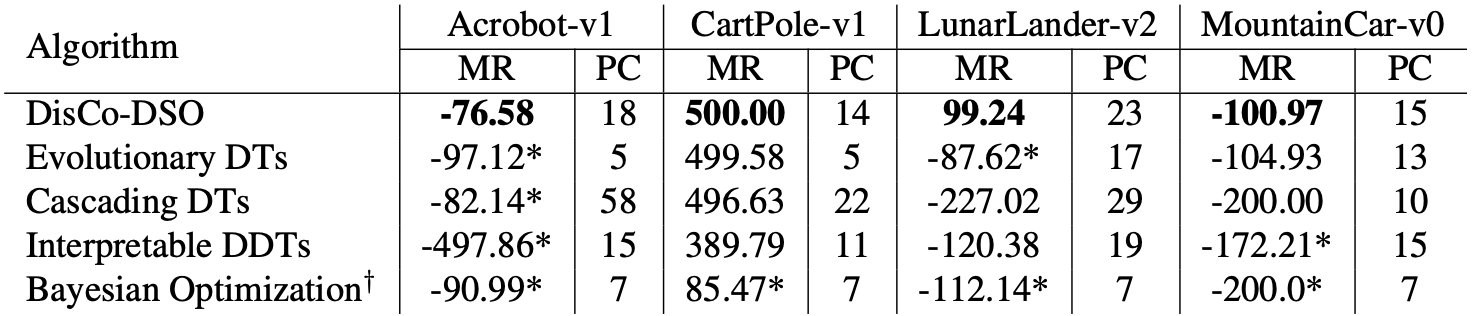
Evaluation of the best univariate decision trees found by DisCo-DSO and other baselines on the decision tree policy task. Here, MR is the mean reward earned in evaluation over a set of 1,000 random seeds, while PC represents the parameter count in each tree. For models trained in-house (*), the figures indicate the parameter count after the discretization process. † The topology of the tree is fixed for BO..
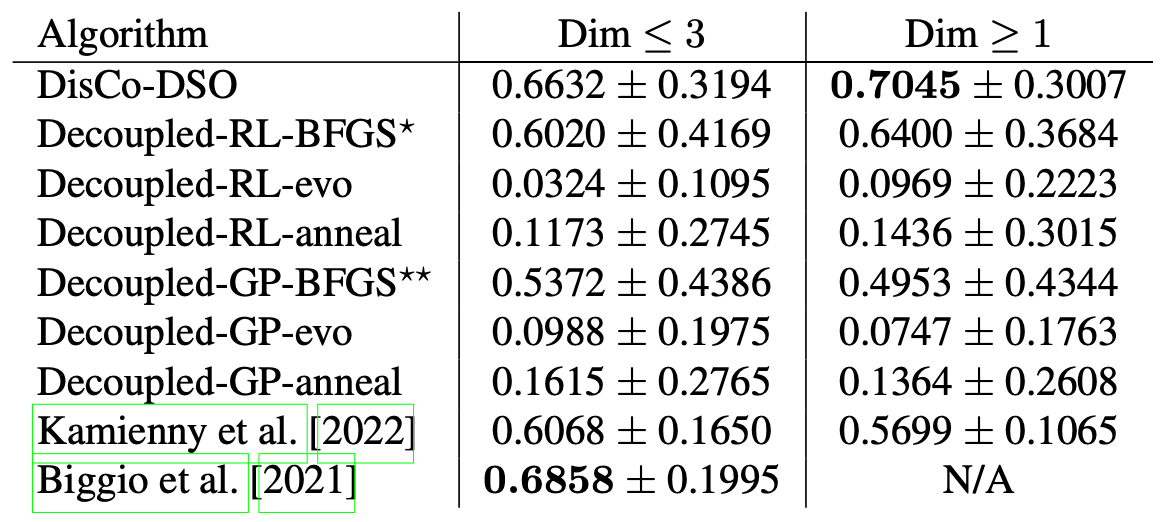
Comparison of DisCo-DSO against decoupled baselines and the methods proposed in Biggio et al. [2021] and Kamienny et al. [2022] on the symbolic regression task. Values are mean ± standard deviation of the reward across benchmarks (see Table 6 of the paper's appendix). We group benchmarks because Biggio et al. [2021] is only applicable to ≤ 3 dimensions. * Petersen et al. [2021a]. ** Koza [1994].
By jointly optimizing hybrid designs, DisCo-DSO achieves:
- Higher accuracy.
- Reduced computational cost.
- Improved interpretability.
Conclusion
DisCo-DSO represents a significant step forward in hybrid discrete-continuous optimization:
- Joint Optimization: Discrete and continuous variables are optimized together, leading to holistic designs.
- Efficiency: Fewer objective evaluations reduce computational burden.
- Flexibility: Robust to black-box, non-differentiable tasks.
This method holds immense potential for advancing interpretable AI, symbolic regression, and decision tree learning, pushing the boundaries of hybrid generative design.
📄 Read the full preprint: preprint
